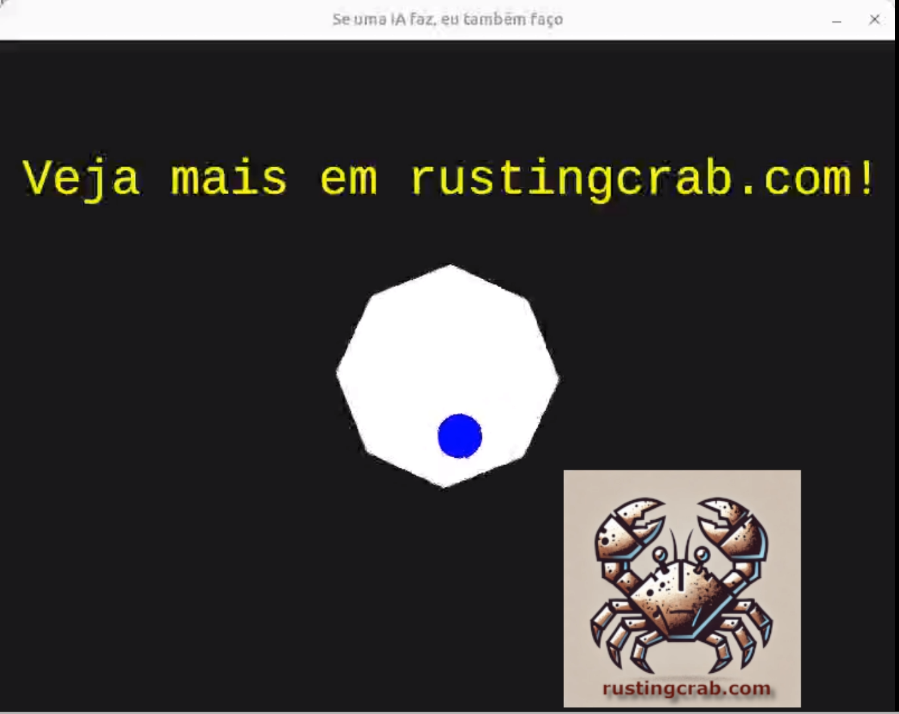
Simulação Física com Octógono Giratório

Bombou por aí essa demo para testar IA. Houve variações com quadrado e octógono. Quando vi, achei um excelente desafio para fazer com Rust e ggez. Depois de muita p0rr@da consegui fazer e documentei tudo para você.

Depois de fazer, pedi para algumas IAs fazerem demo semelhante e todas erraram feio. Há muitos detalhes que só um programador humano consegue resolver.

O código

Este código demonstra uma simulação física simples utilizando a biblioteca gráfica ggez em Rust. Um octógono gira continuamente enquanto uma bola quica em suas bordas, com detecção de colisão e física básica. O código demonstra conceitos de transformações geométricas, vetores e renderização 2D (tudo matemática de ensino médio, mas não é mole não!).

A documentação está em comentários dentro do código-fonte.

Estruturas Principais
- Estado: Controla o estado global do jogo, armazenando:
  - octogono: Objeto gráfico do octógono
  - rotacao_octogono: Ângulo atual de rotação (em radianos)
  - bola: Objeto da bola com física
- Bola: Gerencia a física e propriedades da bola:
  - Posição, velocidade, raio
  - Temporização para controle de quiques
  - Lógica de colisão com as bordas
Funções Chave
- Bola::update():
  Aplica gravidade (980 pixels/s²) e atualiza a posição. Permite quiques a cada 0.5 segundos.
- Bola::verificar_colisao_ajustar():
  Detecta colisões usando projeção vetorial. Calcula o ponto mais próximo nas arestas do octógono e ajusta a posição/velocidade da bola.
- Estado::update():
  Atualiza a rotação do octógono (1 radiano/segundo) e transforma seus vértices usando trigonometria.

Cálculos Trigonométricos

A rotação do octógono é calculada para cada vértice usando:

let rot_x = ponto.x * cos(θ) - ponto.y * sin(θ);
let rot_y = ponto.x * sin(θ) + ponto.y * cos(θ);

θ: Ângulo de rotação acumulado
cos/sin: Funções trigonométricas para rotação 2D
Após a rotação, os pontos são transladados para o centro da tela (400, 300).

Transformações Geométricas

Rotações:
- Cada vértice do octógono é rotacionado individualmente.
- Mantém-se o centro geométrico fixo durante a rotação.
Colisões:
- Conversão entre sistemas de coordenadas: nalgebra → mint → ggez.
- Reflexão do vetor velocidade usando produto escalar para simular quique.

Sobre o ggez

Biblioteca leve para criação de jogos 2D em Rust.
Funcionalidades usadas:
- Gerenciamento de janela e contexto gráfico
- Renderização de formas básicas (círculos, polígonos)
- Sistema de coordenadas e transformações
- Loop principal de jogo (EventHandler)

Se você quiser ver uma demonstração que eu fiz com ggez **abra o projeto ferris_hunter.

Como Executar

Pré-requisitos
- Rust e Cargo instalados (rust-lang.org)

Passos

# Clone o projeto (ou crie os arquivos manualmente)
git clone [URL_DO_REPOSITORIO]

# Entre no diretório
cd projeto

# Execute (o Cargo cuidará das dependências)
cargo run --release

Controles
- A simulação é automática.
- Feche a janela para encerrar.

Resultado Esperado

Janela 800x600 com fundo escuro.
Octógono branco girando no centro.
Bola azul quicando nas bordas.

rustingcrab